Recent efforts in data-driven methods face challenges of the need for hard-to-obtain supervision and issues with high variance in gradient estimations, leading to slow convergence and highly sub-optimal solutions. We address these issues by reformulating MTSP as a bilevel optimization problem, using the concept of imperative learning (IL). This involves introducing an allocation network that decomposes the MTSP into multiple single-agent traveling salesman problems (TSPs). The longest tour from these TSP solutions is then used to self-supervise the allocation network, resulting in a new self-supervised, bilevel, end-to-end learning framework, which we refer to as imperative MTSP (iMTSP). Additionally, to tackle the high-variance gradient issues during the optimization, we introduce a control variate-based gradient estimation algorithm. Our experiments showed that these innovative designs enable our gradient estimator to converge \(20\) times faster than the advanced reinforcement learning baseline, and find up to \(80\%\) shorter tour length compared with Google OR-Tools MTSP solver, especially in large-scale problems, e.g., \(1000\) cities and \(15\) agents.
Imperative Learning
The framework of our self-supervised MTSP network. The allocation network uses supervision from the TSP solver, and the surrogate network is supervised by the single sample variance estimator, reducing the gradient variance.
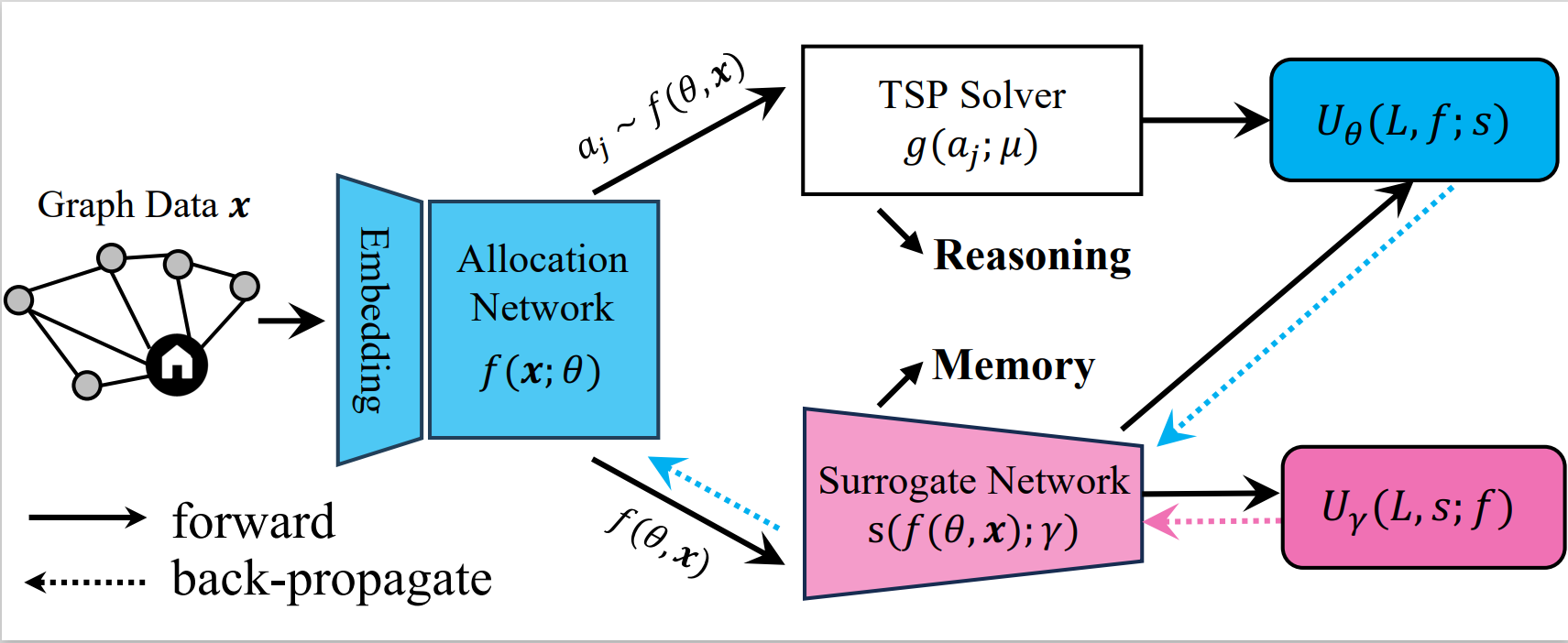
To solve the NP-hard MTSP efficiently, we reformulate MTSP with Imperative Learning, a bi-level optimization-based learning framework. We define \(f\) as the allocation network with parameters \(\mathbf{\theta}\), and \(g\) as the single-agent TSP solver with parameters \(\mathbf{\mu}\). The imperative MTSP (iMTSP) is defined as:
\[\begin{align} & \min_{\theta} U_\theta \left(L(\mu^*), f(\theta); \gamma\right);\quad \min_\gamma U_\gamma\left(L(\mu^*), s(\gamma); \theta\right)\\ & \textrm{s.t.}\quad \mathbf{\mu}^* = \arg\min_\mu L(\mu),\\ & \quad \quad~ L \doteq \max_j D(g(a_j;\mu)), \quad j=1,2,\cdots,M, \\ & \quad \quad~ a_j \sim f(\theta), \end{align}\]where \(a_j\) is the allocation for agent \(j\) sampling the probability matrix by row, and \(L\) returns the maximum route length among all agents. \(s\) is a surrogate network with parameter \(\gamma\).
Optimization
The major challenges for the back-propagation of the proposed framework are the non-differentiability of the TSP solver and the fact that city allocations \(a_j\) vary in a discrete space. These obstacles can be dealt with the log-derivative trick:
\[\nabla_\theta L = L\frac{\partial }{\partial \theta}\log P(\theta),\]where \(L\) is the length of the longest route (i.e., ) returned by the TSP solver \(g\), and \(P\) is the allocation probability matrix returned by the allocation network \(f\). However, the gradient estimated by the log-derivative trick suffers from high variance, leading to slow variance and highly sub-optimal solutions. To address this issue, we introduce a learnable surrogate network \(s\) (control-variate) to reduce the gradient variance significantly. The upper-level objectives for the allocation network are designed as:
\[U_\theta \doteq [L(\mu^*) -L^\prime]\log P(\theta)+s(P(\theta);\gamma),\]where \(L^\prime\) is the surrogate network’s output. The surrogate network is trained directly using the variance of gradients passing to the allocation network, i.e., the objective is:
\[U_\gamma \doteq \rm{Var}( \frac{\partial U_\theta}{\partial \theta}).\]Thus, the gradient for the parameters in the allocation network is: \(\frac{\partial U_\theta}{\partial \theta}=[L(\mu^*)-L^\prime]\frac{\partial }{\partial \theta}\log P(\theta)+\frac{\partial }{\partial \theta}s(P(\theta);\gamma).\) The gradient for the surrogate network’s parameters is: \(\frac{\partial U_\gamma}{\partial \gamma} = \frac{\partial}{\partial \gamma}\mathbb{E}[ (\frac{\partial U_\theta}{\partial \theta})^2]-\frac{\partial}{\partial \gamma}\mathbb{E}[ \frac{\partial U_\theta}{\partial \theta}]^2 = \frac{\partial}{\partial \gamma}\mathbb{E}[ (\frac{\partial U_\theta}{\partial \theta})^2].\)
Experiments
The animation below presents the trajectories in two instances with 5 agents and 500 cities. From the left to the right, are the results corresponding to the proposed iMTSP, the RL baseline, and Google’s ORTools
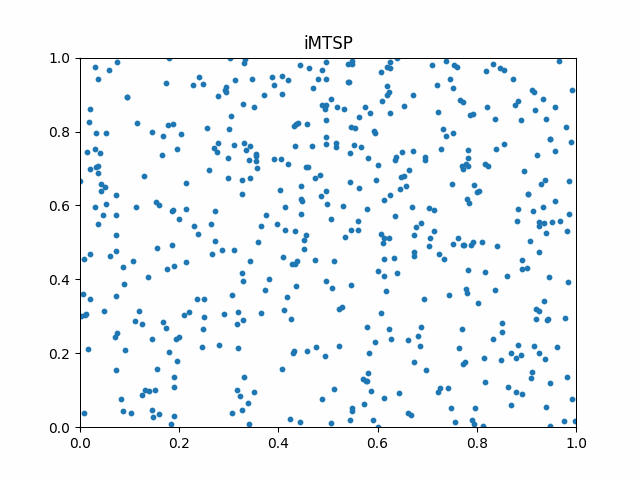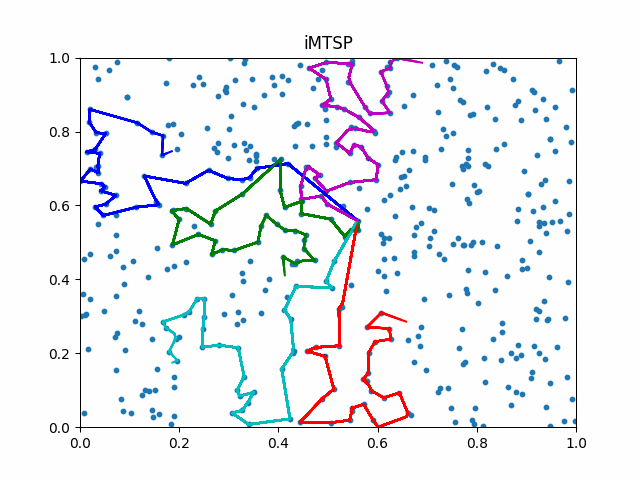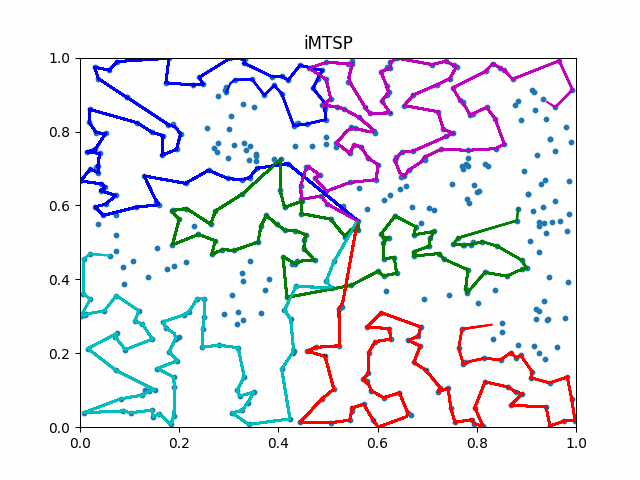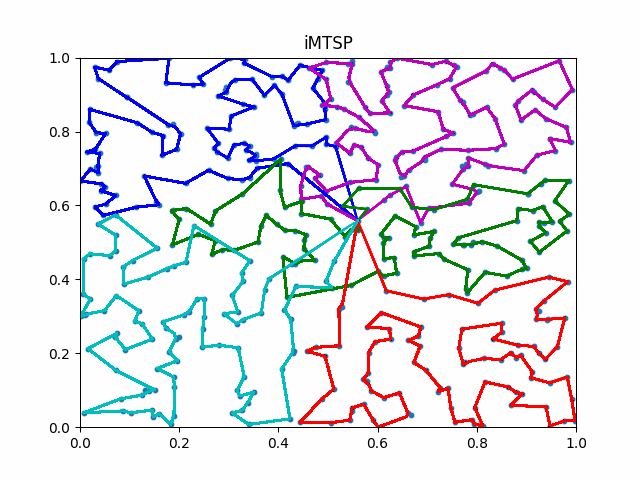
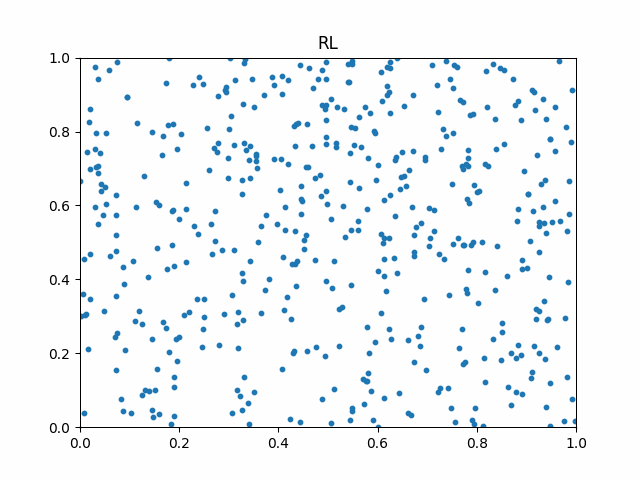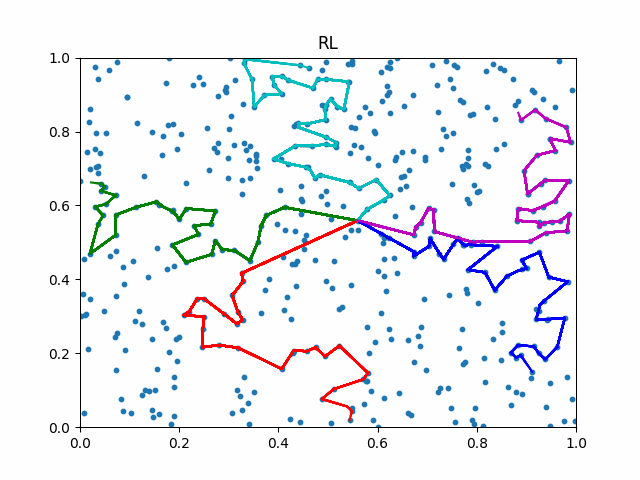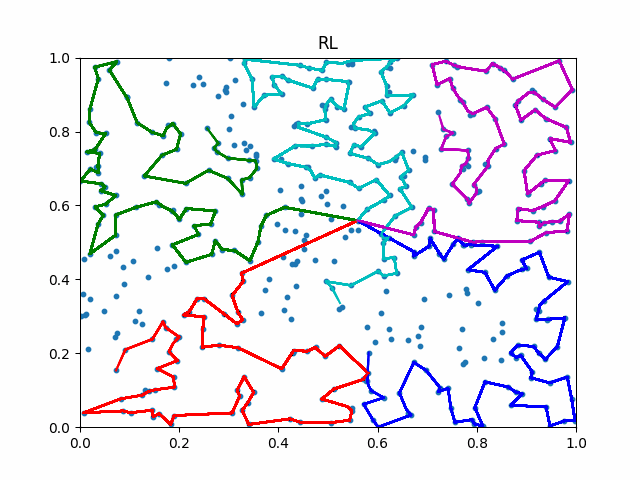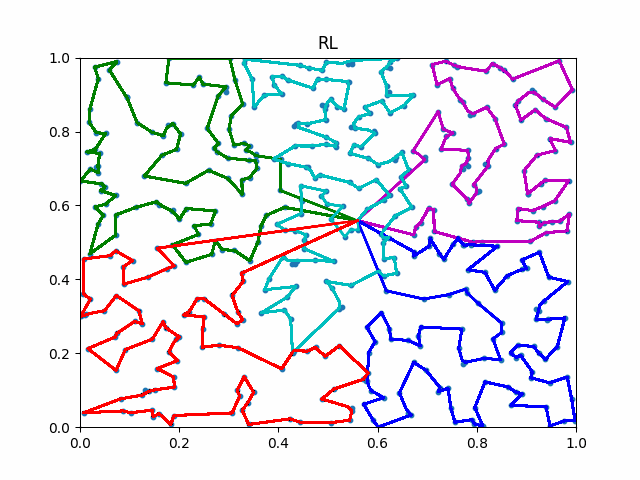
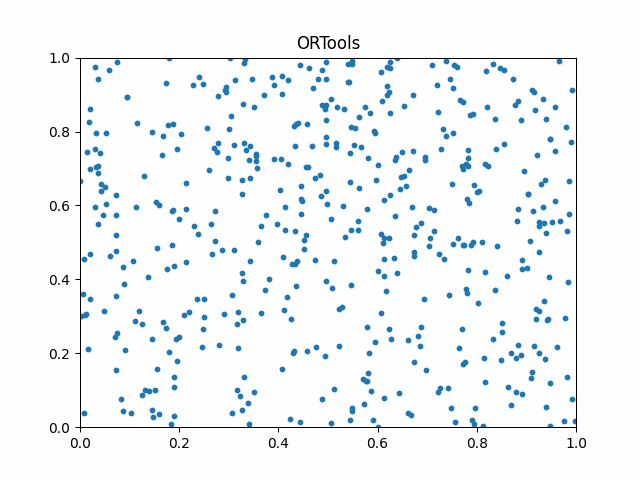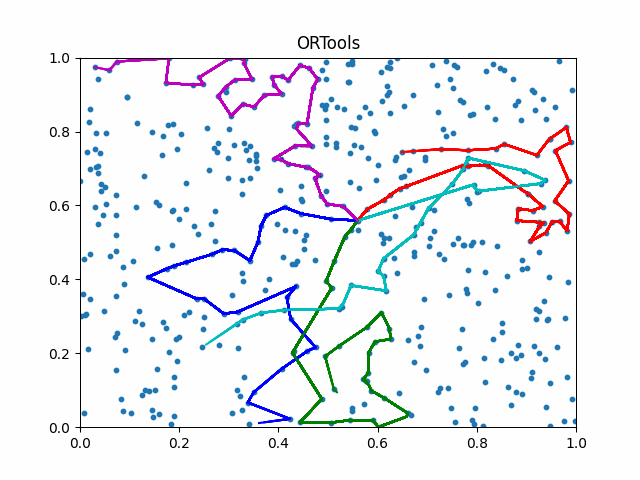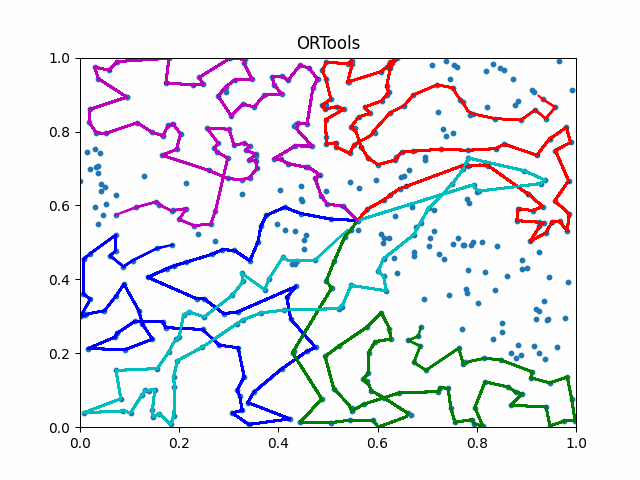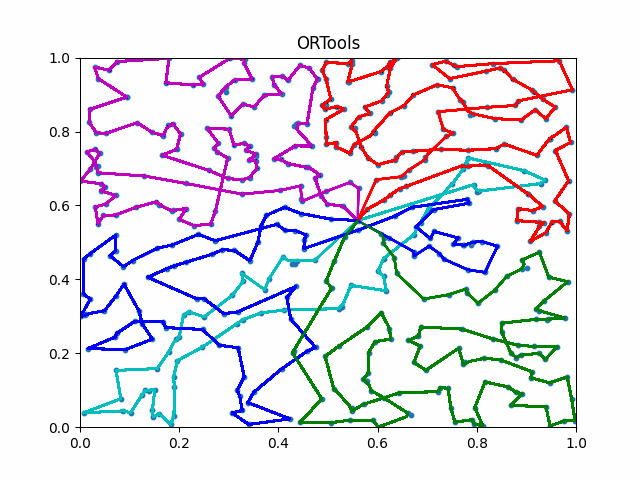
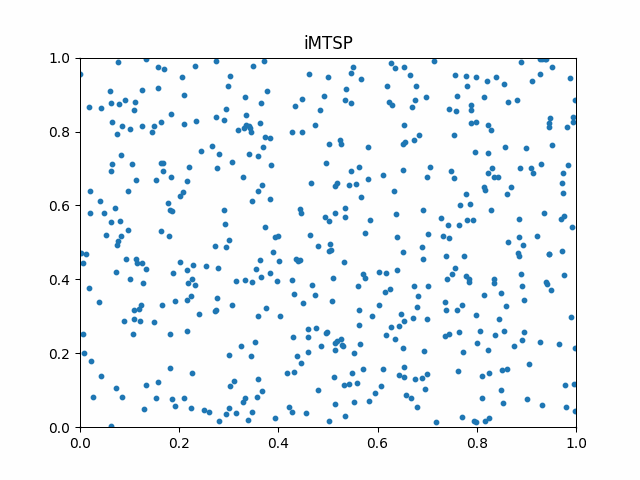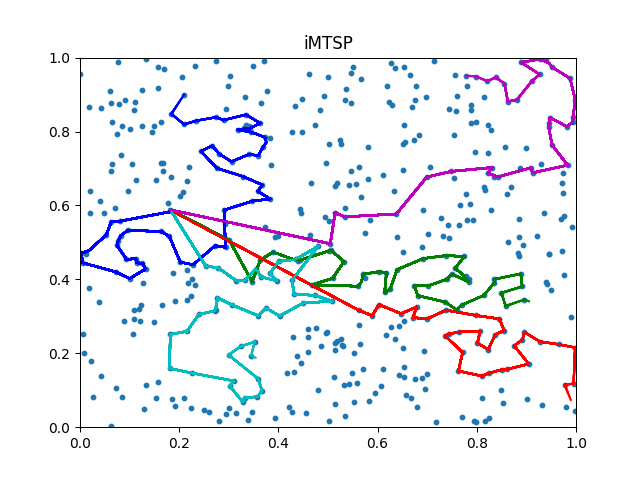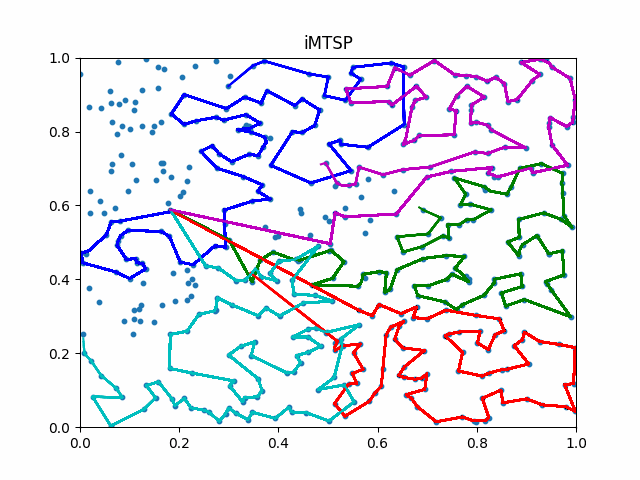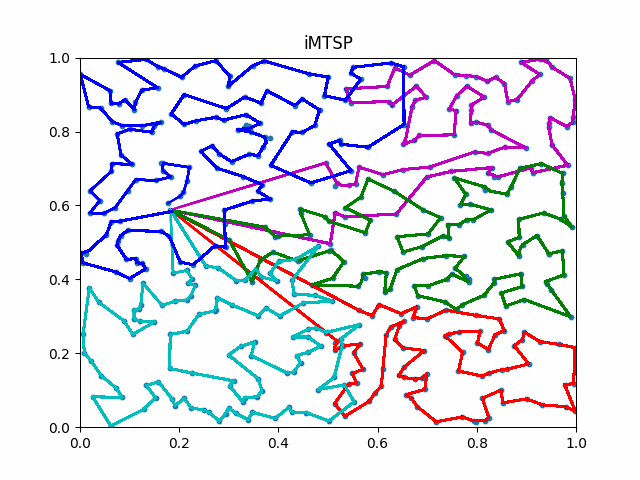
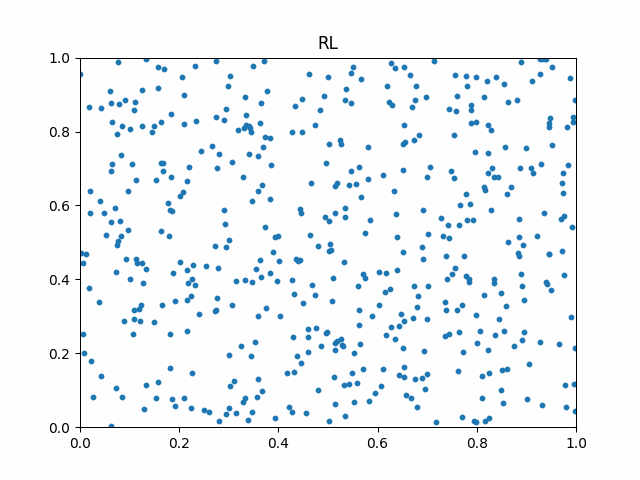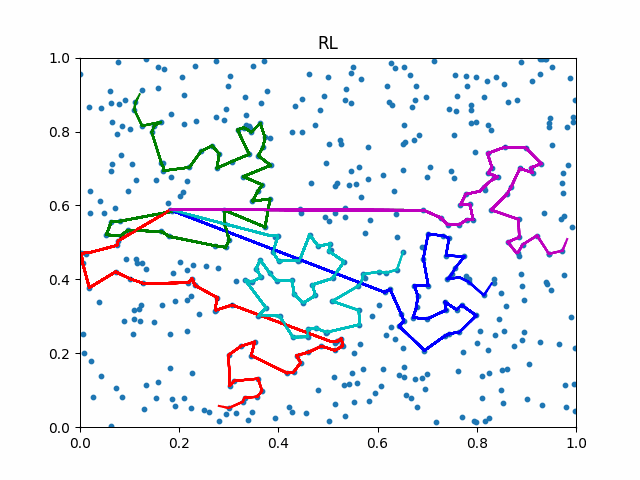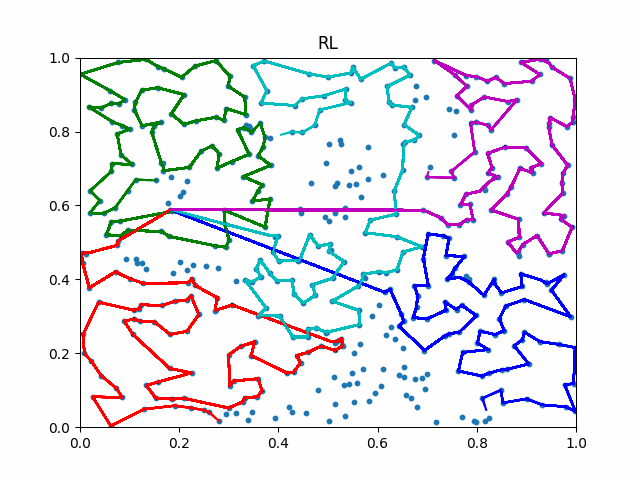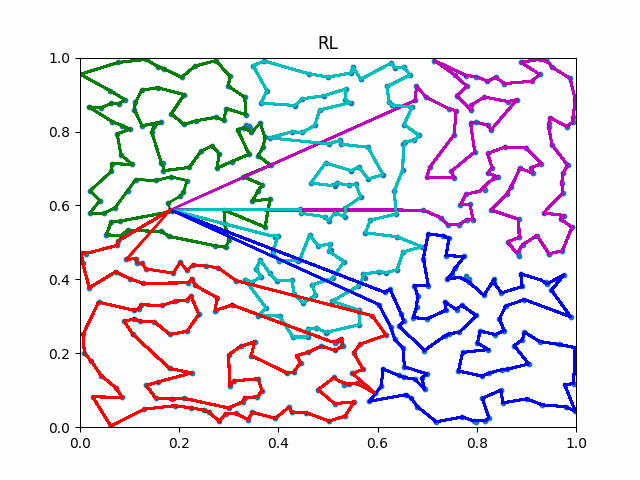
Since all the agents move with constant speed, a shorter running time indicates better performance.
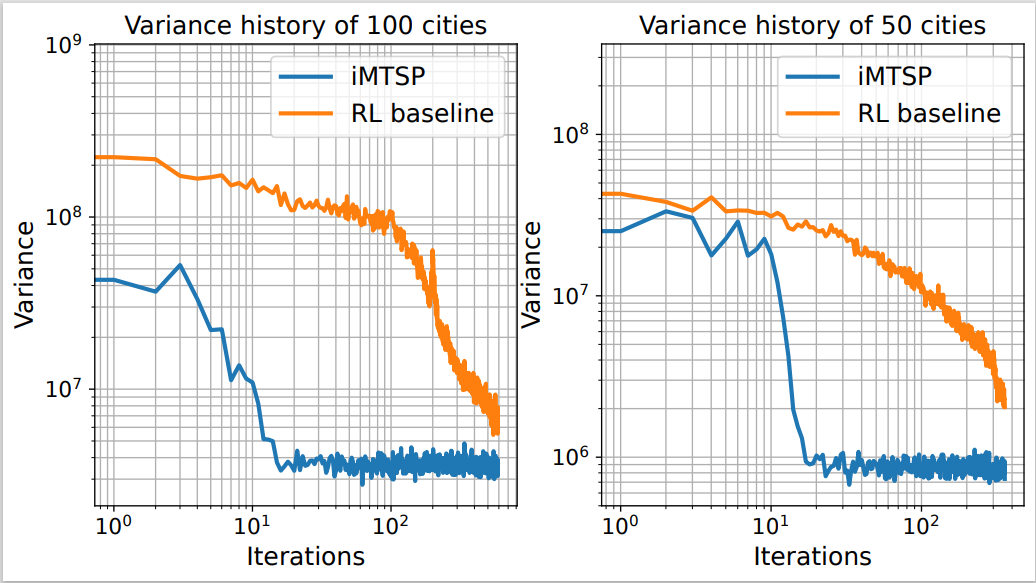
The gradient variance is significantly reduced with the surrogate network serving as a control variate. We explicitly record the mini-batch gradient variance of two training processes with 50 and 100 cities respectively.
Publications
-
iMTSP: Solving Min-Max Multiple Traveling Salesman Problem with Imperative Learning.IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 10245–10252, 2024.


