Simultaneous Localization and Mapping (SLAM) stands as one of the critical challenges in robot navigation. Recent advancements suggest that data-driven methods are highly effective for front-end tasks, while geometry-based methods continue to be essential in the back-end processes. However, such a decoupled paradigm between the data-driven front-end and geometry-based back-end can lead to sub-optimal performance, consequently reducing system capabilities and generalization potential. To solve this problem, we proposed a novel self-supervised imperative learning framework, named imperative SLAM (iSLAM), which fosters reciprocal correction between the front-end and back-end, thus enhancing performance without necessitating any external supervision.
Bi-level Optimization
The framework of iSLAM consists of three parts, i.e., an odometry network \(f_\theta\), a map \(M\) and a pose graph optimization.
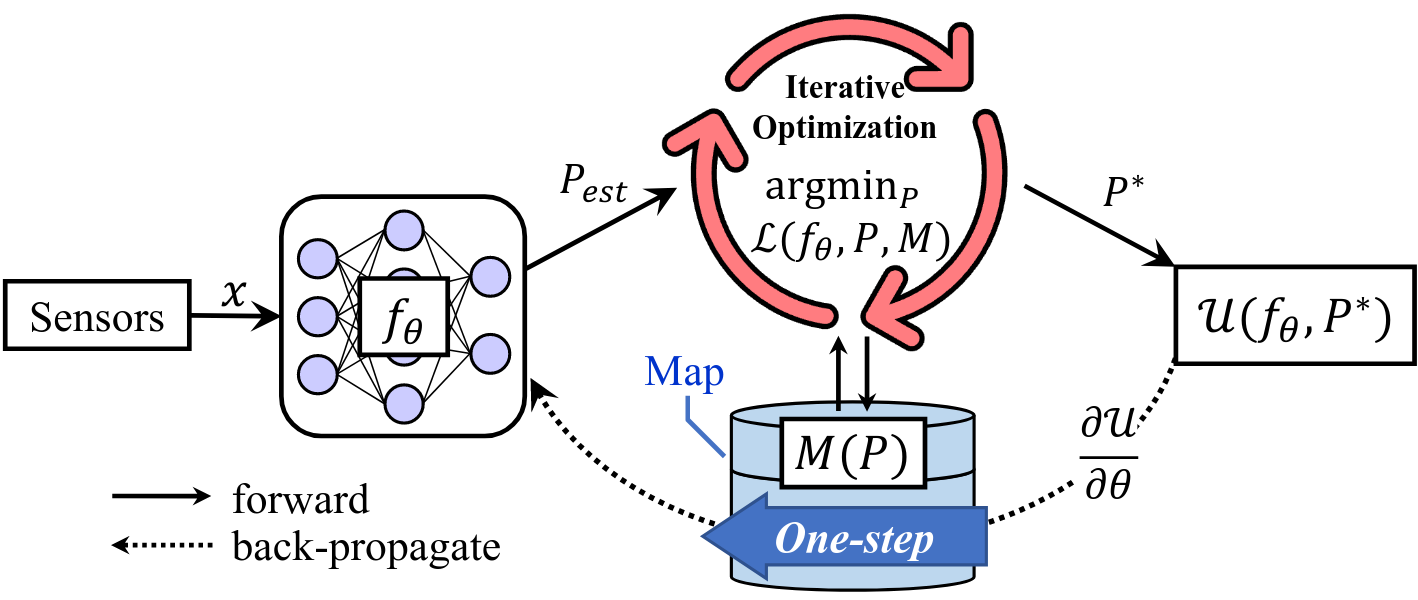
To achieve co-optimization between the front-end and back-end, we formulate the SLAM task as a bi-level optimization problem,
\[\begin{align} \min_\theta& \;\; \mathcal{U}(f_\theta, \mathcal{L}^*), \\ \operatorname{s.t.}& \;\; P^*=\arg\min_{P} \; \mathcal{L}(f_\theta, P, M). \end{align}\]where \(P\) is the robot’s poses to be optimized and \(\mathcal{U}\) and \(\mathcal{L}\) are the higher-level and lower-level objective functions, respectively. \(P^*\) is the optimal pose in the low-level optimization, while \(\mathcal{L}^*\) is the optimal low-level objective, i.e., \(\mathcal{L}(f_\theta, P^*, M)\). In this work, both \(\mathcal{U}\) and \(\mathcal{L}\) are geometry-based objective functions such as the pose transform residuals in PVGO. Thus the entire framework is label-free, which leads to a self-supervised framework. Intuitively, to have a lower loss, the odometry network will be driven to generate outputs that align with the geometrical reality, imposed by the geometry-based objective functions. The acquired geometrical information is stored in the network parameter \(\theta\) and map \(M\) for future reference and to contribute to a more comprehensive understanding of the environment. This framework is named “imperative SLAM” to emphasize the passive nature of this process.
One-step Back-propagation
To supervise the front-end, we need to compute the gradient of higher-level objective \(\mathcal{U}\) w.r.t. network parameter \(\theta\). According to the chain rule,
\[\frac{\partial\mathcal{U}}{\partial\theta} = \frac{\partial\mathcal{U}}{\partial f_\theta}\frac{\partial f_\theta}{\partial\theta} + \frac{\partial\mathcal{U}}{\partial \mathcal{L}^*}\left(\frac{\partial \mathcal{L}^*}{\partial f_\theta}\frac{\partial f_\theta}{\partial\theta} + \frac{\partial \mathcal{L}^*}{\partial P^*}\frac{\partial P^*}{\partial\theta}\right).\]The challenge lies in the last term \(\frac{\partial P^*}{\partial \theta}\), which is very complicated due to iterative solutions of optimization. If we directly go backward along the forward path, we need to unroll the iterations, which is inefficient and also error-prone due to numerical instabilities. Thus, we apply an efficient “one-step” strategy that utilizes the nature of stationary points to solve this problem. We find that after the lower-level optimization converges, \(\frac{\partial \mathcal{L}^*}{\partial P^*} \approx 0\), which eliminates the complex gradient term and bypasses the lower-level optimization iterations. This technique allow the back-propagation to be done in one-step.
Front-end Odometry
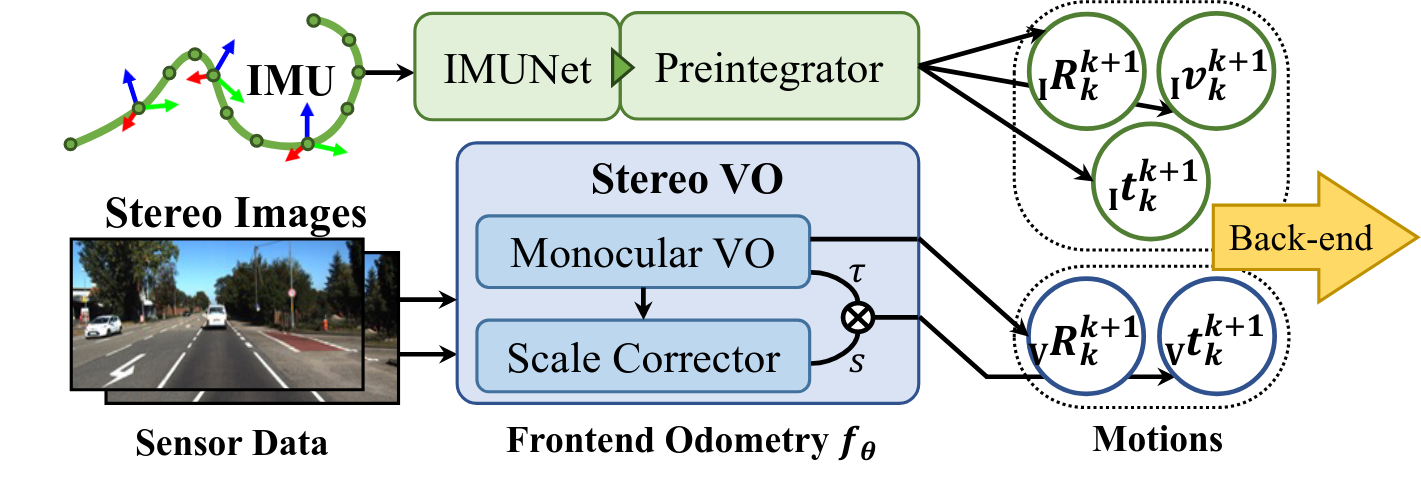
Our front-end odometry includes an IMU module and a VO network to estimate the frame-to-frame motions from IMU measurments and stereo images, respectively. The The stereo VO has a monocular VO backbone and a scale corrector, while the IMU module has a denoising network and a pre-integrator. The entire structure is differentiable to enable imperative learning. The estimated motions are transmitted to the back-end for optimization.
Back-end Pose-velocity Graph Optimization
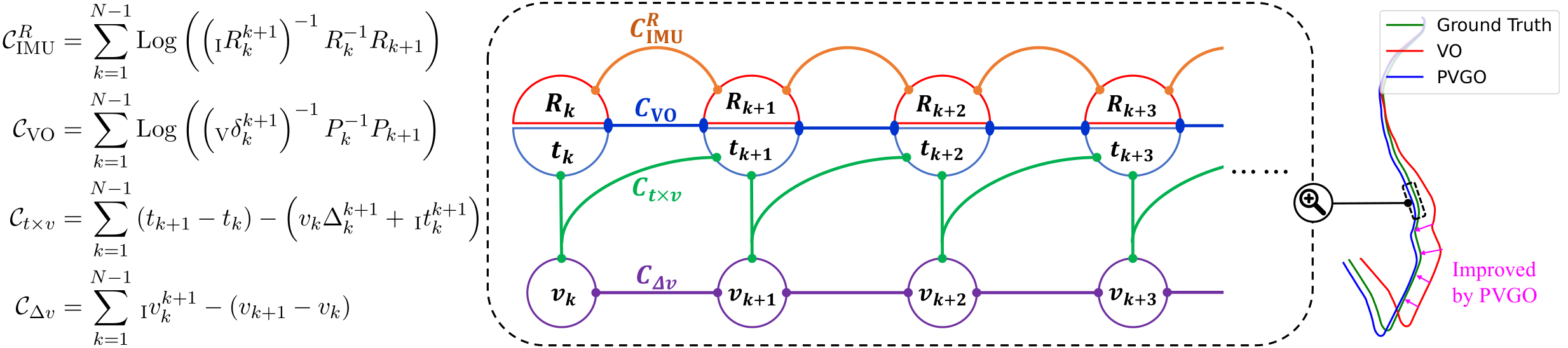
In back-end we employ a pose-velocity graph optimization to integrate the estimations from visual and inertial odometry and jointly contributes to a more accurate trajectory. The optimization variables, i.e., poses and velocities, are nodes in the graph, which are connected by four type of geometric constraints. The graph optimization objective, also the lower-level objective \(\mathcal{L}\), is the weighted sum of these four constraints. The upper-level objective \(\mathcal{U}\) is selected to be identical to \(\mathcal{L}\) for simplicity (they’re not necessarily the same in general cases).
Experiments
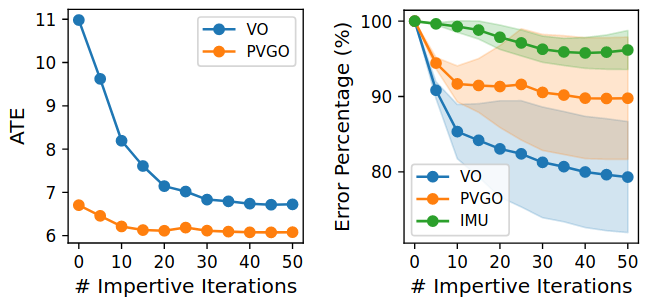
The figure below shows how much the trajectory error (ATE) decreases through imperative learning. It is seen that after several iterations, the ATE of the front-end VO and IMU models reduced by 22% and 4% on average, respectively. Meanwhile, the accuracy of the PVGO back-end also improves by about 10%.
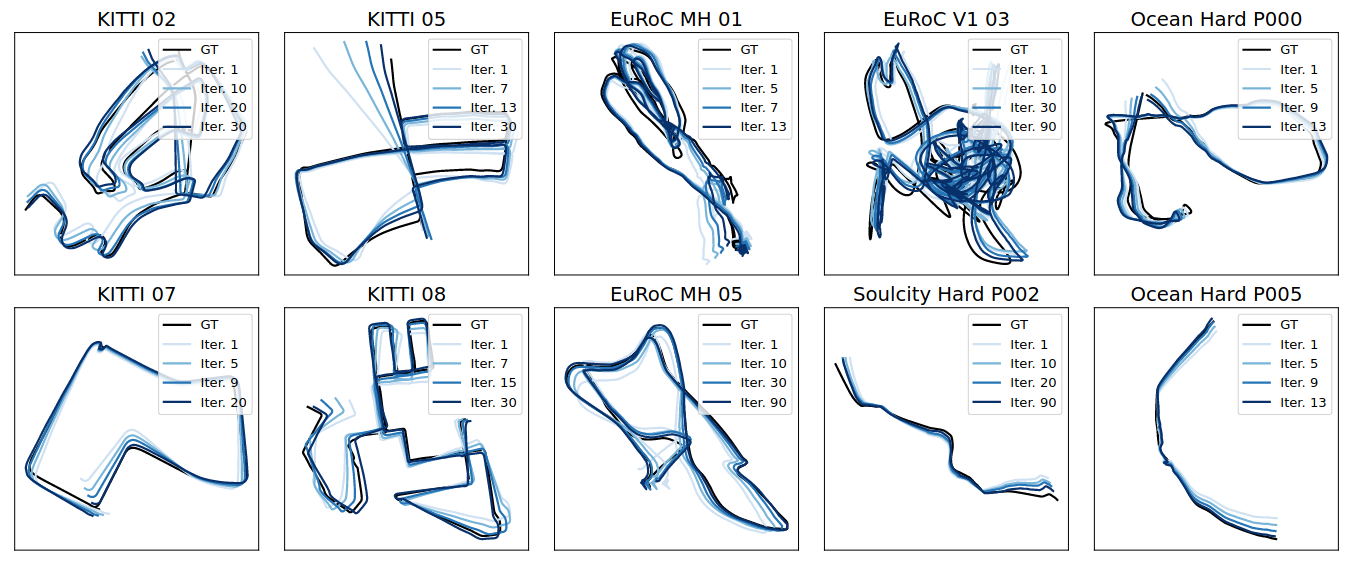
The improvement in trajectory estimation of the VO model through imperative learning is visualized below. It is seen that the original estimation (Iter. 0) is adjusted towards the ground truth (GT) after several iterations.
Publications
-
iSLAM: Imperative SLAM.IEEE Robotics and Automation Letters (RA-L), 2024.