Feature correspondence is a crucial task in computer vision, but it remains challenging due to the lack of sufficient pixel-level annotated data for point matching. Existing methods to alleviate this data problem, such as simulating correspondence annotation or collecting ground truth using specialized equipment, have limitations.

We propose a new self-supervised end-to-end learning framework, called iMatching, for feature correspondence using bilevel optimization and imperative learning. This framework formulates the problem of feature matching as a bilevel optimization problem, where the model parameters are updated through an optimization procedure (bundle adjustment) that is itself an optimization process. This design eliminates the need for ground truth geometric labels and is flexible, lightweight, and generalizable to any up-to-date matching model. We also formulate a specially designed loss function that allows for end-to-end learning without the need for differentiating through the low-level optimization process. Experimental results show that iMatching significantly boosts the performance of state-of-the-art models on pixel-level feature matching tasks.
Bilevel Optimization
The framework consists of a feature correspondence network \(f_{\boldsymbol{\theta}}\) and a bundle adjustment (BA) process. The feature correspondence network produces a set of pixel correspondences, and the BA process seeks to find the optimal camera poses and landmark positions that minimize the total reprojection error.
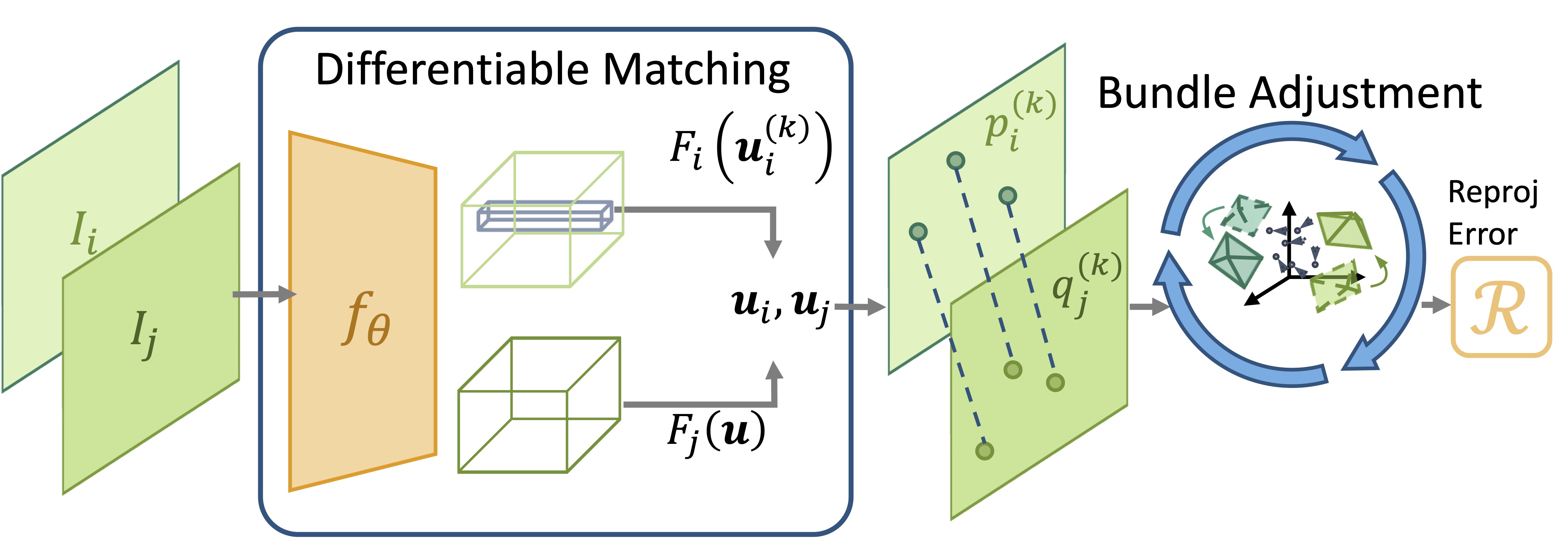
The system is formulated as a bilevel optimization problem, where the upper level optimizes the network parameters \(\boldsymbol{\theta}\) to minimize the reprojection error, and the lower level optimizes the camera poses \(\mathbf{T}\) and landmark positions \(\mathbf{p}\) to minimize the reprojection error given the feature correspondences inferred by the network.
The bilevel optimization problem is expressed as:
\[\begin{aligned} \min_{\boldsymbol{\theta}}& \;\; \mathcal{R}(f_{\boldsymbol{\theta}}; \mathbf{T}^*, \mathbf{p}^*), \\ \operatorname{s.t.}& \;\; \mathbf{T}^*, \mathbf{p}^* = \arg\min_{\mathbf{T}, \mathbf{p}} \mathcal{R}(\mathbf{T}, \mathbf{p}; f_{\boldsymbol{\theta}}), \end{aligned}\]where \(\mathcal{R}\) is the reprojection error function.
Optimization
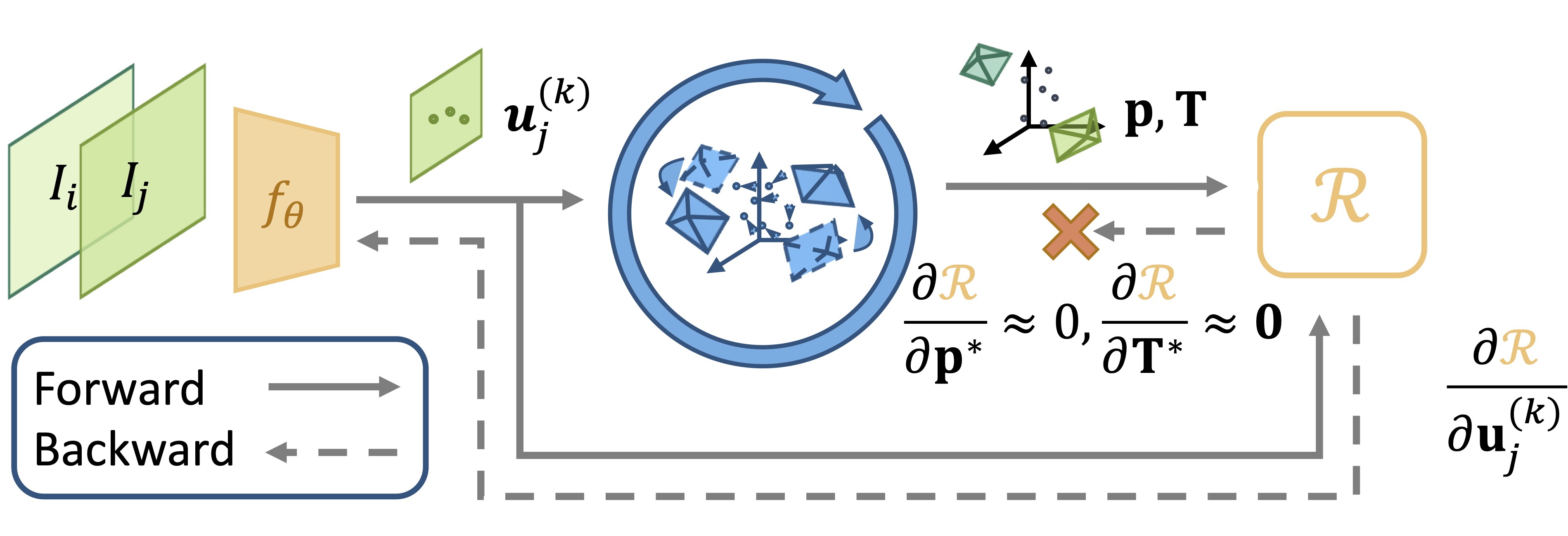
We optimize the feature correspondence network \(f_{\boldsymbol{\theta}}\) via gradient descent. To compute the derivative of the reprojection error w.r.t. the network parameters \(\boldsymbol{\theta}\), we use the chain rule: Here is the revised equation using the standard notation for partial derivatives:
\[\frac{\partial \mathcal{R}}{\partial \boldsymbol{\theta}} = \left( \frac{\partial \mathcal{R}}{\partial \mathbf{T}^*} \frac{\partial \mathbf{T}^*}{\partial f_{\boldsymbol{\theta}}} + \frac{\partial \mathcal{R}}{\partial \mathbf{p}^*} \frac{\partial \mathbf{p}^*}{\partial f_{\boldsymbol{\theta}}} + \frac{\partial \mathcal{R}}{\partial f_{\boldsymbol{\theta}}} \right) \frac{\partial f_{\boldsymbol{\theta}}}{\partial \boldsymbol{\theta}}.\]However, this equation is only well-defined if the feature correspondence network is differentiable and the bundle adjustment (BA) process is also differentiable. The method is compatible with expectation-based matching prediction and regression-based matching prediction.
To make the BA process differentiable, we leverage the optimization of BA at convergence, which allows us to efficiently backpropagate the gradient through the lower-level optimization without compromising its robustness. Specifically, the gradient can be simplified to:
\[\frac{\partial \mathcal{R}}{\partial \boldsymbol{\theta}} = \frac{\partial \mathcal{R}}{\partial f_{\boldsymbol{\theta}}} \frac{\partial f_{\boldsymbol{\theta}}}{\partial \boldsymbol{\theta}}.\]This implies that it is sufficient to evaluate the Jacobian of the reprojection error only once after bundle adjustment and back-propagate through the correspondence argument, treating \(\mathbf{T^*}\) and \(\mathbf{p^*}\) as given.
Experiments
iMatching demonstrates strong performance gains in feature matching and relative pose estimation tasks on unseen, image-only datasets. In terms of practicalness, it preserves the original model’s inference efficiency. Compared to state-of-the-art (SOTA) models, iMatching finetuning boosts performance by an average of 30% and a maximum of 82% on pixel-level feature matching.

Publications
-
iMatching: Imperative Correspondence Learning.European Conference on Computer Vision (ECCV), pp. 183–200, 2024.


